o I’ve been making some good progress on my Ray Casting Engine – which is technically what a Wolfenstein engine is, and I thought it’d be fun to write how I did it. It’s a large, complex engine and didn’t come about over night. In fact, as I’d never written one of these before, I spent about a month (in the evenings) working out how to do it in the first place, before even starting on any Z80.
Believe it or not, I actually wrote 3 different versions before touching Z80, and then a further 2 to help debug it. but more on that later….
I did buy the Wolfenstein engine book, but actually, didn’t really need it. What I ended up using was this website.
https://lodev.org/cgtutor/raycasting.html
This was a great place to start, as it gives a workable demo, but I needed a framework to put it into. I went with GameMaker: Studio 2, as I’m intimately familiar with it, and it meant i could jump right in. This gave me a screen size of 640×480 (same as the demo)
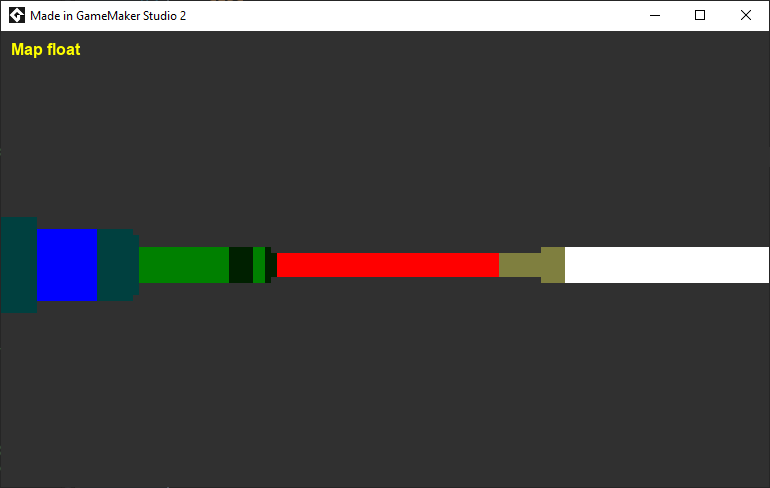
Once I’d cut and paste (pretty much), the example into GameMaker, I could start to try and figure out how it was working. The goal was to get the maths down to 8.8 fixed point, so that it would fit in Z80’s 16bit registers, and I could handle the maths quickly. But before doing that, I needed to do a 16.16 fixed point version. Doing this meant I could verify that it worked, without getting too close to the maths limits, as 8.8 would be cutting pretty close. In fact these were both 15.16 and 7.8 “signed”, as vectors etc would be in all directions, and so could be negative.
Converting to fixed point is pretty straight forward, basically for all 16.16 numbers, you have to multiply all numbers by 65536, or use a <<16. So 15.453 would be 15.453<<16 which is 1,012,727 or $F73F7 in HEX. I personally think of all numbers in hex, as $F73F7 ( $000F_73F7 ), where $000F is the whole number (which is 15), and $73F7 is the fraction. This is perfect, because it means to get the whole number, you just have to take the upper 16bits, usually by doing a >>16.
There’s a heap of pages on fixed point maths, so I’ll just say here that the basics are when you multiply a 16.16 number by another 16.16 number, you then >>16 to get the final answer. So…
var a = $F73F7; // 15.453
var b = $83687; // 8.213
var ans = (a*b)>>16; // == $7EEA54 (126.9153)
And that’s basically it. So after converting to 16.16 (as shown below), I was happy to try and get it into 8.8
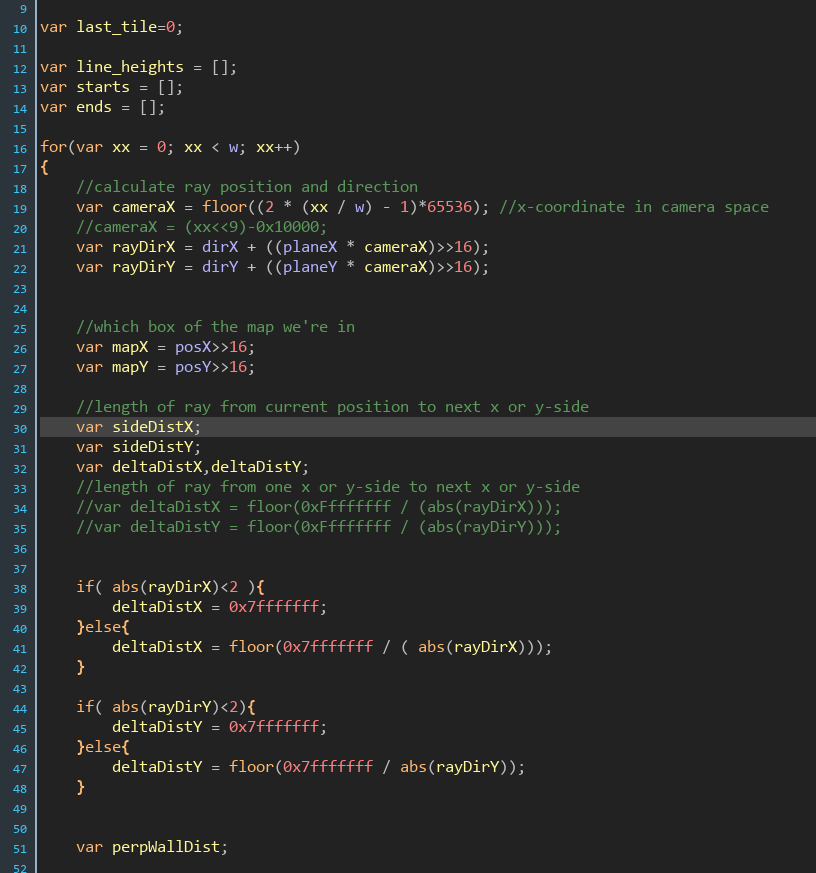
This simply meant copying the above code and doing shifts of 8 rather than 16. I did also have to reduce the screen size to 128×76, down from 640×480 that the demo used. The original Wolfie used 304×152, we’re a little under quarter the size. But since I can only hold a number from 0 to 127 in 7.8, and as I’m targeting the Spectrum Next’s “lores” mode (127×96), then this all fits pretty snugly.
Once I swapped everything over to use >>8 and <<8 type maths, I started noticing the odd missing line on the screen. This turned out to be when DX or DY was 0 exactly – stepping on the axis exactly. This is due to the maths no longer being accurate enough. There are times when you do a 1/X so that you can avoid lots of divisions (i.e. 10*0.5, is faster than 10/2 as 1/2 = 0.5). In 7.8 fixed point you really need to do $10000/X, but that’s out of range, so I’m stuck with doing $7fff/X. This has knock on effects, but you can cope with them later. Note: technically it’s $100, but as you need to shift up by 8 before doing an actual divide in fixed point, that makes it $10000, which is what is out of range, so you’re stuck with $7FFF.
After porting to 7.8 I did hit another issue, rotating the player’s view was going “nuts”. This was because the original demo rotated a vector constantly, and while floating point could handle the accuracy, 7.8 just “drifted” and these vectors stretched and went bizarre. To combat this, I created a table of 256 angles using floating point, and then taking it down into 7.8 fixed point for storing. This means the player now has an “angle” he’s facing, and I simply look up a perfect vector for that angle.
Once I had these issues fixed up, I started to do a Z80 port, only to discover GameMaker doesn’t really do the job of fixed point-ing properly. This is due to the typeless nature of GameMaker, and that many calculations are either done in doubles, or 64bit. This isn’t useful for my needs, I need something very strongly typed, so that I can make sure it all “fits”, before taking the leap into Z80.
So….. I needed a C/C++ or C# framework, where I could use Int16‘s directly. I decided to rip the guts out of my #CSpect framework, and use that to give me a basic bitmap and keyboard input. I then ported ALL GameMaker code (bot 8.8 and 16.16 versions!) over to C# so I had a good debugging framework.
One extra bit I needed to do in C#, was to deal with signed >>8. C/C++ and C# doesn’t do signed shifts the way Z80 does, so I wrote a small signed shift right function to use instead of a simple >>8. This will be replaced in Z80 with actual shifts if needed, although usually you just take the top 16 bits directly and need no shifts at all.
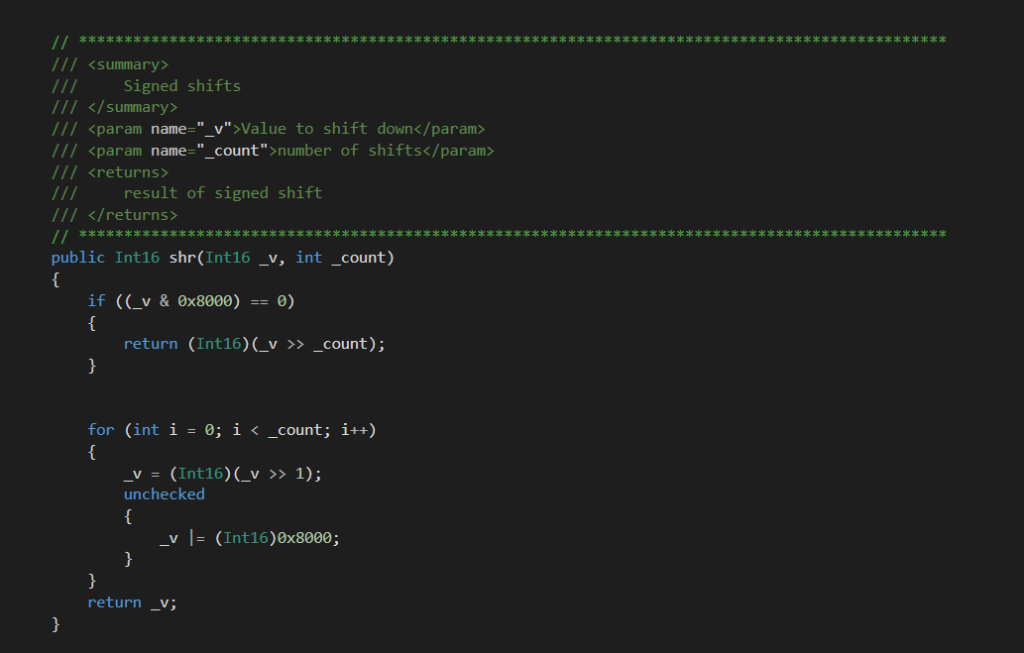
The signed shift function isn’t fancy, it’s just designed to work as I’d expect….
Once all THAT was done…. Actually, I want to just pause here. It may seem like I’m just through stuff together at a great rate of knots, but saying “I’ll just do this…. there, done that”, actually this all took some time. In all, I spent about a month, reading about the engine, and getting these prototypes up and running. It’s important to know there is effort involved in this like this, no matter how experienced you are, you still need to do the grunt work. And this is all BEFORE doing any Z80 at all really!!
Now that all this “prep” work was done….. I’d figured out how the engine worked – mostly, I have a prototype that I could step through along with the Z80 one, so that I could see what answers the Z80 should be giving – this is invaluable on any complex bit of code (and if you don’t fully understand the engine). My goal is to almost line for line port the C#, so that should mean the answers and variables should get exactly the same answers. So stepping the Z80 and C# will give exactly the same answers, and if they don’t, then the Z80 is wrong and I’ll be able to figure out why.
Now comes the hard bit…. writing the Z80 port!