Now we had the prototype, the first thing to do was a direct port to Z80. To do this, I went through each line of the C# like this…
// calculate ray position and direction
//x-coordinate in camera space
// Int16 cameraX = (Int16)(2 * ((xx << 8) / screen_width) - 0X100);
short cameraX = (short)(xx <<<< 2);
cameraX = (short)(cameraX - 0x100);
and wrote an untested Z80 version – like this
ld a,0
AllLines:
ld (xx),a
; Int16 cameraX = (Int16)(2 * ((xx << 8) / screen_width) - 0X100);
; cameraX = (short)(xx << 2);
; cameraX = (short)(cameraX - 0x100);
ld l,a
ld h,0
add hl,hl ; x/128
add hl,hl ; *2
ld de,$100
xor a
sbc hl,de
ld (cameraX),hl
I added the C# code in as comments in order to keep track – as there’s a LOT of code to put in, it’s also a great reference when doing the actual port and looking for bugs.
The next thing I needed was a fast, signed 16bit x 16bit multiply. I got an unsigned one from the Z80 C library, and I then needed to make it a signed version. Signed multiples are easy enough, you simply XOR the top 2 bits of each value, and remember if it’s a 1 or not. You then take the ABS() of these values and multiply them using the “unsigned” 16×16 multiple… then on exit, if the xor answer from the start was 1, you negate the answer. Job done.
; ****************************************************************************************
; multiplication of two 16-bit numbers into a 32-bit product
;
; enter : de = 16-bit multiplicand = y
; hl = 16-bit multiplicand = x
;
; exit : hlde = 32-bit product
; carry reset
;
; uses : af, bc, de, hl
; ****************************************************************************************
Mul_16x16:
ld b,l ; x0
ld c,e ; y0
ld e,l ; x0
ld l,d
push hl ; x1 y1
ld l,c ; y0
; bc = x0 y0
; de = y1 x0
; hl = x1 y0
; stack = x1 y1
mul ; y1*x0
ex de,hl
mul ; x1*y0
xor a ; zero A
add hl,de ; sum cross products p2 p1
adc a,a ; capture carry p3
ld e,c ; x0
ld d,b ; y0
mul ; y0*x0
ld b,a ; carry from cross products
ld c,h ; LSB of MSW from cross products
ld a,d
add a,l
ld h,a
ld l,e ; LSW in HL p1 p0
pop de
mul ; x1*y1
ex de,hl
adc hl,bc
ret
With this done, I could now do the basic 16 bit maths I needed like this…
; var rayDirX = dirX + ((planeX * cameraX)>>8);
ld hl,(cameraX)
ld de,(planeX)
call SMul_16x16 ; exit : hlde = 32-bit product
ld h,l
ld l,d ;>>8
ld de,(dirX)
add hl,de
ld (rayDirX),hl
You can see, that once it’s fit into 8.8 maths, a lot of of complexity falls away. Aside from the 16×16 multiply, you can see the shift 8 is actually just taking the whole byte from one register to another. This basic process is relatively quick, however you have to do hundreds of them – which is the real speed issue we’ll need to tackle later.
There’s a few of these “blocks” to convert, but the biggest target was the delta stepping. It’s important to get that as fast as possible. There are 3 different stepping functions, X axis, Y axis, and a general that moves across both axis at once – this is the one that’ll be hardest to optimise and keep the speed up with. It’s important to get this one as fast as possible, because stepping across the map until you hit a block will be executed hundreds if not thousands of times, especially in large open rooms.
So here’s the C# code I need to port…..
while (true)
{
//jump to next map square, OR in x-direction, OR in y-direction
if (sideDistX < sideDistY)
{
sideDistX += deltaDistX;
mapX += stepX;
side = 0;
}
else
{
sideDistY += deltaDistY;
mapY += stepY;
side = 1;
}
//Check if ray has hit a wall
int map_index = (mapY * MAP_WIDTH) + mapX;
last_tile = map.worldMap[map_index];
if (last_tile != 0) break;
}
I spent some time fiddling with register layouts and the rest, trying to keep it all in registers as memory access is painful.
; --------------------------------- General ---------------------------
; while (true)
; jump to next map square, OR in x-direction, OR in y-direction
ld a,(mapX)
ld c,a
ld a,(mapY)
ld b,a
ld a,(stepX)
ld d,a
ld a,(stepY)
ld e,a
exx
ld hl,(sideDistX) ; 16
ld iy,(sideDistY) ; 20
ld de,(deltaDistX) ; 20
ld bc,(deltaDistY) ; 20
ld ixl,$30 ; side
xor a ; and at the end of the loop clears carry
@KeepLooping:
; if (sideDistX < sideDistY)
ld a,l ; 4
sbc a,iyl ; 8
ld a,h ; 4
sbc a,iyh ; 8
jr nc,@ix_greaterthan
; sideDistX += deltaDistX;
add hl,de ; 11
;mapX += stepX;
exx ; 4
ld a,c ; get mapX
add a,d ; add stepX
ld c,a
; side = 0;
ld ixl,$30 ; 9Ts ($30 for $3000 base address)
jp @skip_branch
@ix_greaterthan:
;sideDistY += deltaDistY;
add iy,bc ; 15Ts
;mapY += stepY;
exx
ld a,b ; get mapY
add a,e ; add stepY
ld b,a
; side = 1;
ld ixl,$20 ; 9Ts ($20 for $2000 base address)
ld a,c ; mapX
@skip_branch:
ld h,b ; mapY
ld l,0
srl h ; *64
rr l
srl h
rr l
add hl,Map ; 16
add hl,a ; A already mapX
ld a,(hl) ; get map entry
exx
and a
jp z,@KeepLooping
ld (lastblock),a
ld a,ixl
ld (side),a
exx
ld a,b
ld (mapY),a
ld a,c
ld (mapX),a
@FoundBlock:
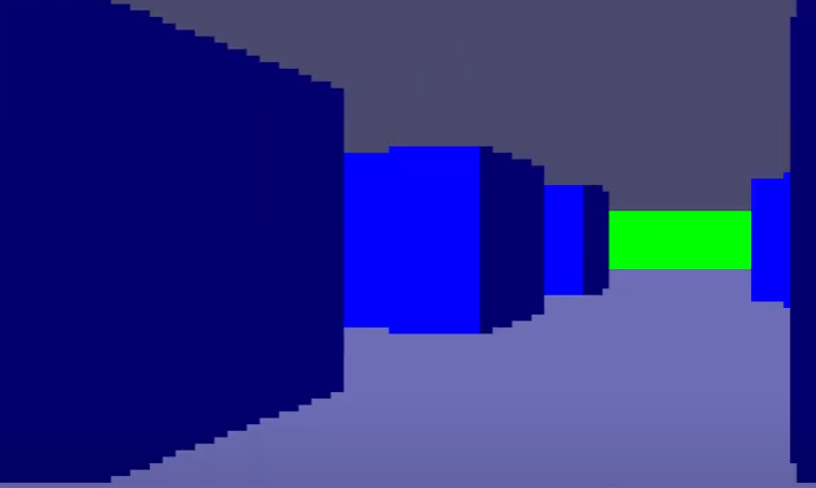
So you can see I’ve managed to keep it all in registers – even though I had to use the alt set, and ix and iy. But that’s still much faster than saving values, and reloading others from memory. The X and Y axis ones are similar, but without the branches and doesn’t need as many registers. The last part is simply working out how how to draw the column and drawing it. This is simply a case of working out the screen address and plotting a vertical line, clipping to the top and bottom of the screen – simple compared to the rest of the stuff we’ve just done! Once that’s done – and once I spent a day or so debugging it and getting it all working, I was left with this….
This was the first publicly shown version, and took about a month and a half of my spare time to get running (more or less).